Быстрый и грубый ответ на вопрос: сколько людей в России заболеет коронавирусной инфекцией COVID-19?
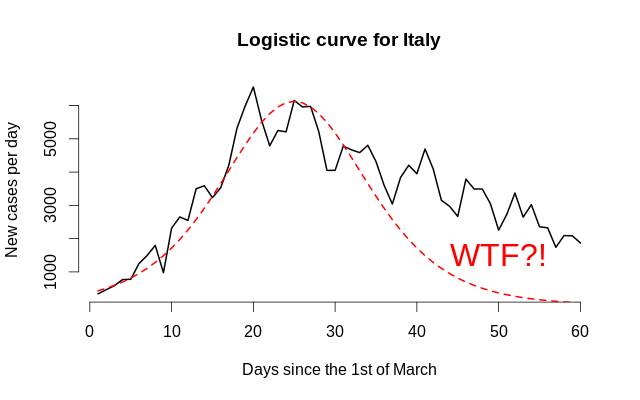
Сегодня мы оценим часто упоминаемую «логистическую кривую» на данных по выявленным заболевшим коронавирусной инфекцией в разных странах, используя эконометрические и численные методы, и рассчитаем сценарные прогнозы.
В России часто слышится вопрос:
— Когда наша страна пройдёт пик?
Это сложный...



















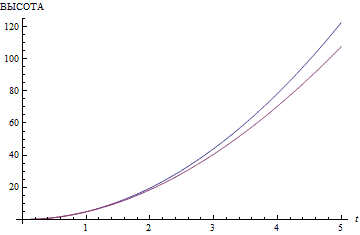
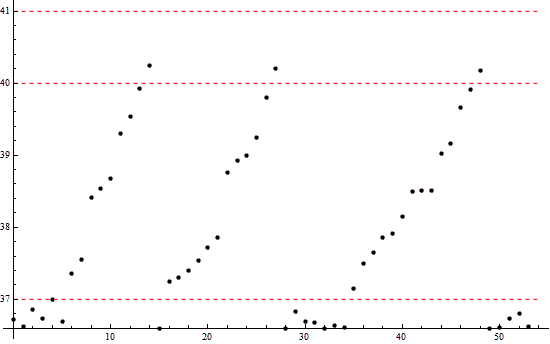






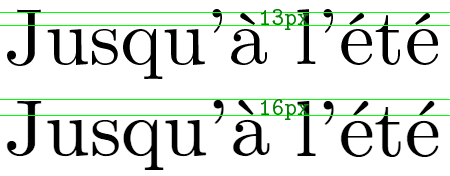


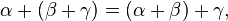
 (Отображение зави...
(Отображение зави...